| Dalla Galleria di Jos Leys |
Le sue opere denotano un uso razionale di poliedri (nostre recenti conoscenze, vero ragazzi di 3°B?) e di altri concetti scientifici e matematici, interpretati in modo personalissimo, con cui ha ottenuto stupefacenti effetti paradossali.
La sua prolifica produzione è intrisa di una notevole componente matematica, di implicazioni logiche, geometriche e fisiche diversificate. Mi soffermo, in questo articolo, sull'impiego dei "Dischi di Poincaré" da parte del "nostro".
Cosa saranno mai?- vi starete chiedendo. Tenetevi forte perché dobbiamo abbandonare la geometria euclidea, a voi nota.
Perché c'è forse una geometria non euclidea? Certo che sì. Ne esistono diverse, in realtà. Basta negare alcuni postulati euclidei, quale il 5° postulato di Euclide (ne esistono diverse formulazioni. Quella più utilizzata oggi è il Postulato di Playfair: "Data una retta r ed un punto P fuori di essa, esiste una ed una sola parallela alla retta r, passante per il punto P") affinché vengano generate geometrie non euclidee.
"Due rette aventi una perpendicolare in comune nelle tre geometrie. Nella geometria iperbolica le rette divergono, ed è quindi possibile trovare molte rette parallele (cioè che non si intersecano). Nella geometria ellittica le rette convergono e quindi non esistono rette parallele."Il Disco di Poincaré è un modello di geometria iperbolica, descritto dal matematico francese Jules Henri Poincaré. La geometria iperbolica, anche denominata geometria della sella o geometria di Lobachevskij, è una geometria non euclidea ottenuta rimpiazzando il postulato delle parallele con il cosiddetto postulato iperbolico.
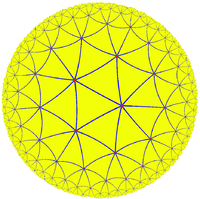 |
| Disco di Poincaré, da Wikipedia. |
Intorno al 1956, Escher esplorò il concetto che mirava a rappresentare l'infinito su un piano bidimensionale. Le discussioni con il matematico canadese H.S.M. Coxeter indirizzò l'interesse di Escher verso le tassellazioni iperboliche, che sono tassellazioni regolari del piano iperbolico.
Il quadrittico delle tassellazioni di Escher su legno, denominate "Limite del cerchio I-IV", dimostrano il concetto di infinito, da lui cercato. Nel 1959, Coxeter pubblicò le sue considerazioni sulle quattro opere di Escher, affermando che erano precise sino al millimetro.
Il belga Jos Leys, ingegnere meccanico e appassionato di matematica, ha realizzato, ispirandosi al "Limite del Cerchio I-IV " di Escher, delle bellissime produzioni iperboliche con il software Ultrafractal.
Ne riporto due dalla sua nutrita galleria.
| E35 by M.C.Escher |
| E70 by M.C.Escher |








Con Escher non si riesce a comprendere se sia la Matematica a farsi arte o viceversa, poi, ragionandoci un po', la risposta arriva da sola: è la Matematica nella sua più alta espressione a presentarsi a noi in forma artistica, ma ci vuole il genio e la sensibilità artistica di eccezionali personaggi come Escher per rendere "l'amalgama" un vero e proprio capolavoro.
RispondiEliminaRimango sempre a bocca aperta ogni volta che vedo qualche opera di questo geniale mate-artista.
Per quanto "uscire" dalla geometria euclidea per i ragazzi (ma non solo) possa necessitare di uno sforzo immaginativo non sempre semplicissimo, fare questi "viaggi", anche solo per breve tempo, fa comprendere quanto la matematica sia fortemente legata anche all'immaginazione oltre che alla semplice osservazione del tangibile. E dopo certi viaggi non si può non amare ancora di più questa fantastica disciplina.
Un salutone
Marco
Concordo in toto. Escher colpisce sempre. E' un artista unico nel suo genere. Matematica ed arte si fondono mirabilmente nelle sue stupefacenti opere e non si può non avvicinarsi all'una e all'altra delle due con stupore, ammirazione e voglia di conoscerle più da vicino.
EliminaGrazie del puntuale commento.
Un salutone.
Annarita
Concordo con Marco queste opere disegnate da Eschier son veramente molto belle ma sopratutto colorate!!!!
RispondiEliminaA domani prof!!:):)
Concordare circa la bellezza delle opere di Escher (senza la i) è piuttosto inevitabile, Sara. Sono espressioni uniche della genialità di un sommo artista...ma non perché "sono soprattutto colorate "!
EliminaA domani.
Stupenda biunivocità fra Matematica e Arte!
RispondiEliminaBenvenuta M.C.S:)
EliminaTi ringrazio del commento di cui condivido il contenuto.
Queste opere sono veramente bellissime. Escher ha disegnato veramente cose bellissime!!!!!
RispondiEliminaCiao
Indubbiamente, Matilde. A domani!
Elimina