 Il celebre pittore tedesco Albrecht Dürer (1471-1528), considerato il massimo esponente della pittura rinascimentale tedesca, ha dato un importante contributo alla conoscenza dei poliedri nel suo libro del 1525, Underweysung der Messung, di cui è disponibile la traduzione in lingua inglese dal titolo Painter's Manual. Quest'opera, uno dei primi libri ad insegnare i metodi della prospettiva, è stato molto considerato in tutto il XVI secolo.
Il celebre pittore tedesco Albrecht Dürer (1471-1528), considerato il massimo esponente della pittura rinascimentale tedesca, ha dato un importante contributo alla conoscenza dei poliedri nel suo libro del 1525, Underweysung der Messung, di cui è disponibile la traduzione in lingua inglese dal titolo Painter's Manual. Quest'opera, uno dei primi libri ad insegnare i metodi della prospettiva, è stato molto considerato in tutto il XVI secolo.
Dürer viaggiò in Italia per apprendere la prospettiva e volle pubblicarne i metodi in modo che non rimanessero appannaggio di pochi artisti. Non si sa con precisione chi abbia appreso dalla sua opera, ma Luca Pacioli probabilmente fu uno di essi. Alcune di queste tecniche e illustrazioni seguono molto da vicino il lavoro di Piero della Francesca.
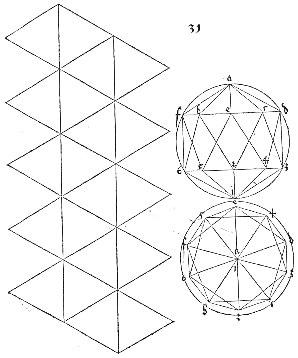
Underweysung der Messung di Düreri contiene una discussione molto interessante sulla prospettiva e su altre tecniche, ed è caratterizzato dall'idea rinascimentale che i poliedri sono modelli degni dell’attenzione di un artista. Elemento ancora più importante, questo libro presenta i primi esempi noti di sviluppi di poliedri. L'immagine sopra è un disegno di Durer dello sviluppo di un icosaedro. Anche se lo sviluppo è corretto, le sue tecniche di prospettiva erano ancora in fase di evoluzione, ed è interessante osservare la presenza di una serie di inesattezze.
A destra, un altro sviluppo di Dürer, che è da interpretarsi come un troncamento di  un cubo troncato. Mentre la maggior parte dei suoi sviluppi sono abbastanza precisi, questo contiene un errore significativo, che si noterà se verrà osservato accuratamente per qualche istante. Otto dei vertici (quelli in alto a sinistra e in alto a destra dei quattro dodecagoni centrali) indicano un valore di 360 gradi degli angoli intorno ad essi, e così non possono piegarsi come previsto. Questo dovrebbe far comprendere che l'idea di uno sviluppo non è così semplice e ovvia come si potrebbe supporre.
un cubo troncato. Mentre la maggior parte dei suoi sviluppi sono abbastanza precisi, questo contiene un errore significativo, che si noterà se verrà osservato accuratamente per qualche istante. Otto dei vertici (quelli in alto a sinistra e in alto a destra dei quattro dodecagoni centrali) indicano un valore di 360 gradi degli angoli intorno ad essi, e così non possono piegarsi come previsto. Questo dovrebbe far comprendere che l'idea di uno sviluppo non è così semplice e ovvia come si potrebbe supporre.
Una interessante proprietà di questo poliedro è la seguente: se i dodecagoni sono regolari allora possono essere inscritti in una sfera.
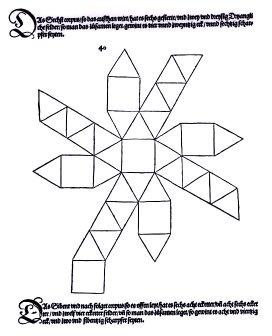 Underweysung der Messung è significativo anche perché l’edizione rivista del 1538 contiene le prime presentazioni del cubottaedro troncato e del cubo camuso. Il cubo camuso è il primo dei due solidi Archimedei chirali ad essere stato riscoperto nel Rinascimento. (L’altro, il dodecaedro camuso, ha dovuto attendere Keplero). Data la chiralità del cubo camuso (vedere un'immagine), sembra strano che Durer non abbia lasciato una raffigurazione del solido né citato le due versioni di questo. Egli si accontentò dello sviluppo a sinistra.
Underweysung der Messung è significativo anche perché l’edizione rivista del 1538 contiene le prime presentazioni del cubottaedro troncato e del cubo camuso. Il cubo camuso è il primo dei due solidi Archimedei chirali ad essere stato riscoperto nel Rinascimento. (L’altro, il dodecaedro camuso, ha dovuto attendere Keplero). Data la chiralità del cubo camuso (vedere un'immagine), sembra strano che Durer non abbia lasciato una raffigurazione del solido né citato le due versioni di questo. Egli si accontentò dello sviluppo a sinistra.
Uno dei capolavori di Dürer, l'incisione  Melancholia I, rappresenta un pensatore frustrato che siede su un poliedro raro. Molto è stato scritto, analizzando il simbolismo nell’immagine e il possibile significato di ogni elemento, compreso il poliedro. Si potrebbe speculare che il cubo rappresenti la mascolinità e che quello troncato in posizione verticale potrebbe contenere una qualche simbolismo freudiano.
Melancholia I, rappresenta un pensatore frustrato che siede su un poliedro raro. Molto è stato scritto, analizzando il simbolismo nell’immagine e il possibile significato di ogni elemento, compreso il poliedro. Si potrebbe speculare che il cubo rappresenti la mascolinità e che quello troncato in posizione verticale potrebbe contenere una qualche simbolismo freudiano.
Geometricamente, il poliedro è semplicemente un cubo o romboedro, troncato nel vertice superiore. (Non è facile stabilire se il vertice inferiore è anche troncato in modo che il solido poggia su una faccia triangolare, o se il vertice inferiore penetra simbolicamente la terra, ma nessun altro scrittore sembra avallare questa possibilità). Panofsky lo descrive accuratamente come un "romboide troncato".
E’ possibile renderlo proporzionato in modo che i vertici siano proiettati su una griglia quadrata 4-per-4 come quella del quadrato magico.
Schreiber suggerisce che esso derivi da un romboedro con angoli di 72 gradi nelle facce, che è stato troncato in modo da poter essere inscritto in una sfera.
Per coloro che desiderano leggere qualcosa in più, ecco di seguito alcuni riferimenti per iniziare:
- P. J. Federico, "The Melancholy Octahedron," Mathematics Magazine, pp. 30-36, 1972.
- T. Lynch, "The geometric body in Durer's engraving Melancholia I," Journal of the Warburg and Courtauld Inst., pp. 226-232, 1982.
- C. H. MacGillavry, "The Polyhedron in A. Durer's 'Melancolia I': An Over 450 Years Old Puzzle Solved ?" Netherland Akad Wetensch. Proc., 1981.
- E. Panofsky, The Life and Art of Albrecht Durer, Princeton, 1955.
- P. Schreiber, "A New Hypothesis on Durer's Enigmatic Polyhedron in His Copper Engraving 'Melencholia I'," Historia Mathematica, 26, pp. 369-377, 1999.
- K. D. Walton, "Albrecht Durer's Renaissance Connections Between Mathematics and Art," The Mathematics Teacher, pp. 278-282, 1994.
- J. Sharp, "Durer's Melancholy Octahedron," Mathematics in School, Sept. 1994, pp. 18-20.






Ciao Annarita, come va? contraccambio glia auguri per un ottimo anno scolastico ...so che per te sarà così, come sempre..ti scriverò un'email ho bisogno di dirti alcune cose
RispondiEliminaun abbraccio
elisa
C' e' sempre molto da imparare dai tuoi post. Grazie.
RispondiEliminaBuonanotte
Vale
Carissima Annarita , si riprende ed io auguro a te e ai tuoi alunni un buon anno scolastico !!!
RispondiEliminaUn abbraccio
Paola
Va bene, cara Elisa. A presto!
RispondiEliminaUn grazie sincero, cara Paola!
RispondiEliminaUn abbraccio e a presto!
Grazie a te, per il passaggio, Pier.
RispondiEliminaA presto!